BAB3
(PEMERIHALAN DATA DENGAN
BERBAGAI SUKATAN)
Jenis Sukatan:
q Di Bab 2, data diperihalkan dengan illustrusi
(histogram, poligon, carta dsb)
q Dlm bahagian ini, beberapa sukatan
digunakan utk memerihalkan data diperkenalkan;
q Terdapat 4 sukatan;
Sukatan Kecenderungan Memusat
Sukatan Variasi
Sukatan kedudukan
Sukatan Bentuk
Sukatan
Kecenderungan Memusat:
q Histogram, poligon dapat menunjukkan “pusat data” iaitu
lokasi di mana cerapan mempunyai kekerapan yang tinggi.
q 3 ukuran yang memberikan kedudukan pusat data; MIN,
MEDIAN, MOD
q Min
Purata bagi semua nilai-nilai yg mungkin baik dalam populasi atau sampel.
Min populasi: purata semua nilai-nilai mungkin dalam populasi, ditandakan
sebagai m, satu kuantiti tetap & biasanya tidak diketahui dan
merupakan parameter bagi sesuatu populasi.
Min sampel: purata cerapan-cerapan dalam sampel; Penganggar titik kepada
min populasi, bukan tetapan iaitu berubah mengikut sampel; mempunyai taburan
kebarangkalian tersendiri.
Jika Y1, Y2, Y3, …, YN adalah nilai-nilai yang mungkin dalam satu populasi, maka min populasi ditakrifkan sebagai
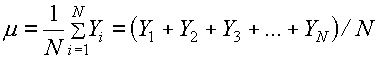
Jika y1, y2, y3, …, yn adalah cerapan-cerapan dalam sampel bersaiz n, maka
Min
sampel,
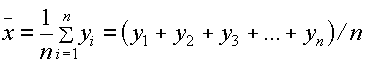
Min
sampel adalah penganggar takpincang (unbiased) kepada min populasi.
![]()
q Median
“pusat” data bertertib (ordered data)
Jika bil. cerapan n ganjil
Median,
Md=cerapan bertertib ke - (n+1)/2
Conth: 2,4,5,12,2
Data bertertib: 2,2,4,5,12
Md=cerapan
bertertib ke- (5+1)/2=4
Jika bil. cerapan genap
Median,
Md= purata antara dua cerapan di tengah data bertertib
Conth: 3,5,7,10
Md=(5+7)/2=6
q
Kesensitifan Kepada Cerapan-cerapan Ekstrim (Outlier):
Sukatan min sangat sensitif
kepada nilai-nilai ekstrim berbanding median.
q
Memilih Antara Min & Median.
Lihat taburan kekerapan; Jika simetri, Min adalah lebih sesuai. Jika pencong, Median adalah lebih sesuai.
q
Mod
Nilai atau (nilai-nilai) yang paling kerap
berlaku.
Contoh: 0
0 0 2 3 4
4 4 5 5 6 7;
4 paling kerap berlaku & mod bagi data ini adalah 4.
Mod tidak semestinya di pusat data;
Contoh: 0
0 0 0 2 2
3 4 4 5 6 di mana mod=0 & bukan di pusat data.
Mod mungkin berguna jika data mempunyai dua
taburan (bimodal)
Contoh: 1
1 1 4 7 7 7
; di sini ada dua mod iaitu 1 dan 7 dengan kekerapan yang sama &
menunjukkan taburan bimodal.
Sukatan Variasi:
q
Pertimbangkan 3 sampel berikut:
X: 5,5,1,75,75,79
Y:40,40,40,40,30,50
Z:40,40,40,40,39,41
Min bagi ketiga-tiga sampel adalah sama iaitu 40.
Bagaimana membezakan? Perlu sukatan ubahan.
Sukatan variasi - beri maklumat
ttg. Rebakan cerapan-cerapan.
Rebakan X > rebakan Y > rebakan Z =>
Sukatan variasi X > Sukatan variasi Y > Sukatan variasi Z.
q
4 sukatan berkaitan variasi data; Julat, Sisihan Piawai, Varians dan
Pekali variasi.
q
Julat ditakrifkan sebagai nilai terbesar tolak nilai terkecil.
q
Seperti juga min, sisihan piawai & varians boleh merujuk kepada
populasi atau sampel.
Sisihan piawai & varians populasi: parameter
populasi, ditandakan sebagai s dan s2 & biasanya tidak diketahui.
Sisihan piawai sampel & varians sampel:
penganggar kepada sisihan piawai populasi & varians populasi.
Jika Y1, Y2, Y3,
..., YN adalah ahli-ahli dalam populasi, sisihan piawai populasi
ditakrifkan sebagai
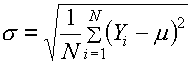
Varians populasi s2 adalah kuasa dua nilai ini.
Jika y1, y2, y3,
..., yn adalah cerapan-cerapan dalam sampel, maka sisihan piawai
sampel,
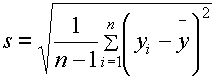
Varians
sampel s2 adalah kuasa dua dari nilai ini.
Perhatikan
pembahagi sisihan piawai sampel adalah n-1 bukannya n.
q
Contoh: Perbandingan berat 2 kumpulan tikus yg didedahkan kepada
persekitaran yg berlainan
|
Persekiataran A (Sampel A) (g) |
22 |
22 |
23 |
24 |
24 |
24 |
24 |
25 |
26 |
26 |
|
Persekiataran B (Sampel B) (g) |
16 |
17 |
20 |
23 |
24 |
25 |
27 |
28 |
29 |
31 |
Gambarajah dot bagi kedua-dua sampel adalah seperti
berikut:
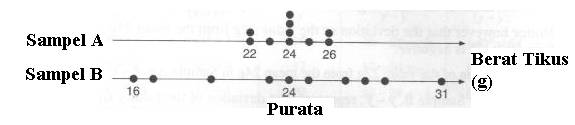
Dari gambarajah, jelas Sampel B mempunyai variasi
lebih besar berbanding variasi Sampel B.
Julat
Sampel A= 26-22=4g
Julat
Sampel B=31-16=15g
Julat Sampel A < Julat Sampel B; Menggambarkan
variasi sampel B lebih berbanding Sampel A.
Pengiraan julat bagaimanapun hanya menggunakan 2
nilai; Nilai terbesar & terkecil, dgn itu tidak dapat memberikan jumlah
variasi bagi semua cerapan.
Sisihan piawai dan varians sampel berdasarkan
formula di atas:
Sisihan
piawai Sampel A: 1.41, Varians A=1.99
Sisihan
piawai Sampel B: 5.06, Varians B=25.6
q
Ralat piawai merujuk kepada sisihan piawai min sampel. Formula yg digunakan
adalah:
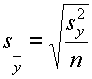
q
Pekali Variasi
Sukatan yang sepatutnya digunakan untuk membandingkan variasi 2 sampel yang mempunyai min yang mempunyai magnitud yang sangat berbeza.
Contoh: Membandingkan variasi ukuran panjang telinga gajah dan variasi ukuran telinga tikus. Pengukuran yg mempunyai min besar mempunyai ke kecenderungan mempunyai variasi besar berbanding pengukuran dgn min kecil.
Formula:
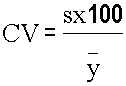
Tafsiran Min sampel & Sisihan Piawai Sampel:
q
Diberi 2 statistik ini, apakah kenyataan yg boleh dibuat? Berapa banyak cerapan berada
dlm. 2 sisihan piawai min?
q
Berapa % data terkandung dlm. di
antara x - s dan x + s atau x - 2s dan
x + 2s?
Kenyataan am boleh dibuat
berdasarkan 2 petua:
Ketaksamaan Chebyshev
Peraturan empirik
q
Ketaksamaan Chebyshev
Tiada andaian ttg. taburan
populasi di mana data dikutip. Kenyataan-kenyataan berikut boleh dibuat:
i.
Sekurang-kurangnya 75% data di antara x-2s dan x + 2s
ii.
Sekurang-kurangnya 89% data di antara x-3s dan x +3s
iii.
Amnya, sekurang-kurang (1-1/k2)x100% antara x-ks dan x+ks,
k=2,3,4, … .
q
Peraturan empirik
lebih terperinci & perlu
andaian ttg. populasi di mana sampel dikutip adalah bertaburan NORMAL (iaitu
taburan btk. Loceng).
i.
Lebih kurang 68% data antara x-s dan x+s
ii.
Lebih kurang 95% data antara x-2s dan x+2s
iii.
Lebih kurang 99.7% data antara x-3s dan x+3s
Sukatan Kedudukan:
q
Menentukan kedudukan sesuatu cerapan berbanding dgn. cerapan lain
q
2 sukatan; Persentil dan Skor-Z
q
Persentil
Persentil ke-p adalah cerapan pada kedudukan di
mana p% cerapan berada pada kedudukan sebelum nilai ini dan (100-p)% berada
selepas.
40% 60%
________________|___________________
data tertib
![]()
persentil
ke -40
Susunkan cerapan menurut tertib menaik.
Kedudukan persentil ke-p=n x
(p/100)
Jika
bukan integer, bulatkan kpd. integer terdekat & persentil ke-p adalah
cerapan pd. kedudukan ini.
Jika
integer, persentil ke-p adalah purata cerapan pd. kedudukan ini dan cerapan
selepas itu.
Contoh: Jika n=125, tentukan
persentil ke-35 & Persentil ke-60
Kedudukan persentil ke-35=125 x (35/100)=43.75.
Bulatkan kpd. interger terdekat iaitu 44.
Maka persentil ke-35=cerapan
bertertib pd. kedudukan ke-44
Kedudukan
persentil ke-60=125 x (60/100)=75
Maka persentil ke-60= purata cerapan bertertib
ke-75 dan cerapan bertertib ke-76.
q
Skor-Z:
sukatan kedudukan mengambil
kira min dan sisihan piawai.
Skor-Z ditakrifkan sebagai
![]()
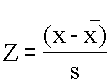
Contoh: Jika ![]() = 1.40 , s=0.15
= 1.40 , s=0.15
Kedudukan cerapan 1.18 mengikut
skor-Z adalah
Z=(1.18
- 1.40)/0.15 = -1.45
Dikatakan cerapan 1.18 adalah
1.45 sisihan piawai ke kiri min.
Sukatan Bentuk:
q
Dlm illustrusi histogram & poligon boleh dilihat kepencongan bentuk
taburan kekerapan
q Kepencongan juga boleh
ditentukan dgn mengira pekali kepencongan; Sukatan menentukan kepencongan
taburan data
q Pekali kepencongan sk,
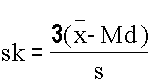
Md=Median
Jika data pencong ke kanan, sk > 0, Pencong ke kiri, sk < 0, Simetri, sk=0.
q Satu lagi sukatan bentuk iaitu
kurtosis sukatan kemuncungan “peakedness” taburan data. Bagaimanapun formulanya
agak rumit & tidak dibincangkan disini.
Pengiraan Min, Sisihan Piawai, Median Daripada Jadual taburan
Kekerapan:
q Diberi taburan kekerapan
(nilai-nilai tanpa cerapan), min dan sisihan piawai boleh dianggarkan.
q Contoh:
|
No Kelas |
Kelas |
Kekerapan |
|
1 |
20 - 30 |
5 |
|
2 |
30 - 40 |
14 |
|
3 |
40 - 50 |
9 |
|
4 |
50 - 60 |
5 |
|
5 |
60 - 70 |
2 |
|
|
Jumlah |
35 |
q
Cerapan sebenar tidak diketahui, tetapi boleh dianggap sama dengan titik
tengah bagi kelas berkenaan.
Contoh: Untuk kelas 1, Titik Tengah=
(20+30)/2=25; Jumlah cerapan dlm. Kelas 1 @ 5 x 25=125.
|
Kelas |
Nilai Tengah |
Anggaran Jumlah Cerapan |
|
1 |
25 |
5 x 25 |
|
2 |
35 |
14 x 35 |
|
3 |
45 |
9 x 45 |
|
4 |
55 |
5 x 55 |
|
5 |
65 |
2 x 65 |
|
|
Jumlah |
1425 |
Anggaran Min sampel=1425/35=40.7
q Untuk mengira varians & sisihan
piawai, perlu anggarkan jumlah kuasa dua.
|
Kelas |
Nilai Tengah |
Anggaran Jumlah Kuasa Dua |
|
1 |
25 |
5 x 252 |
|
2 |
35 |
14 x 352 |
|
3 |
45 |
9 x 452 |
|
4 |
55 |
5 x 552 |
|
5 |
65 |
2 x 652 |
|
|
Jumlah |
62075 |
Anggaran varians sampel=(62075
– (35 x 40.72))/34;
q Median ditentukan dgn
menganggarkan pusat data bertertib.
Md = Nilai bertertib ke- (35+1)/2 = Nilai cerapan bertertib
ke-18
Kelas 1 mengandungi 5 cerapan terkecil & kelas
2 mengandungi 14. Dua kelas pertama mengandungi 19 cerapan. Maka cerapan
bertertib ke-18 berada dlm. kelas kedua iaitu median cerapan ke-13 dlm. kelas
kedua. Kelas kedua bermula pada 30 dgn. lebar kelas 10.
Md = 30
+(13/14)(10)=39.3