Taburan Min Sampel

Jika sampel bersaiz n diambil bagi satu pembolehubah X dari satu populasi dengan taburan tertentu, maka min sampel juga adalah merupakan satu pembolehubah dan mempunyai taburan tersendiri.

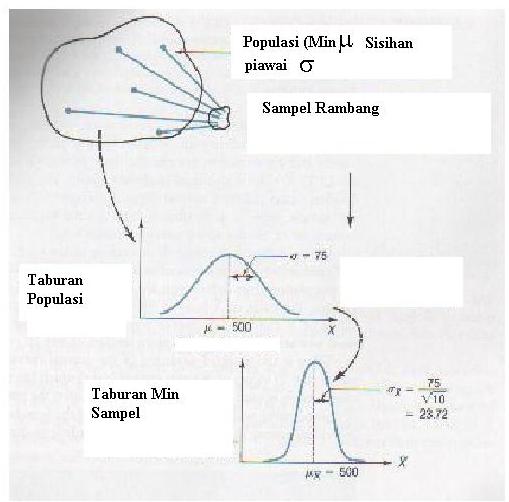
Teorem Had Kecenderungan

Memusat (Central Limit Theorem)

Jika sampel rambang bersaiz n diambil dari populasi yang mempunyai min m dan sisihan piawai s, maka min sampel yang terhasil, akan bertaburan normal dengan min m dan sisihan piawai

s/Ön. Kenyataan ini betul jika X ~ N(m,s²).

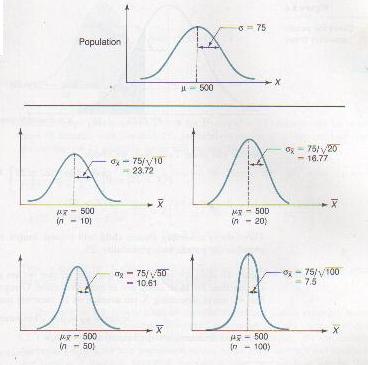
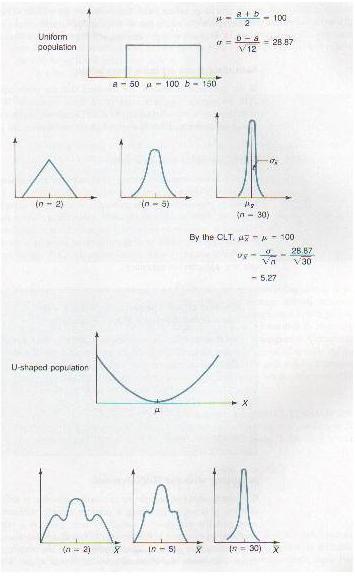
Bagaimanapun jika X tidak bertaburan normal tetapi n > 30, maka ia hanya penghampiran sahaja.

Transformasi

Jika

dan s diketahui, maka pembolehubah Z yang ditakrifkan sebagai

maka Z adalah pembolehubah rambang normal piawai iaitu Z~N(0,1). Dengan cara yang sama jika

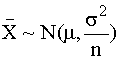(menurut CLT).

Maka

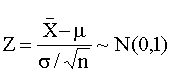
Bagi Kb(Z³Z_o)=g, nilai Z_o boleh ditentukan untuk sebarang nilai g, juga nilai g, boleh ditentukan bagi sebarang nilai Z_o, menggunakan Jadual Taburan Normal Piawai.

Jika sisihan piawai populasi s, tidak diketahui, maka boleh ditakrifkan pembolehubah

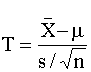
akan beraburan t (n-1), n-1 merujuk kepada darjah kebebasan (dk) berkaitan dengan sisihan piawai sampel, s.

Konsep darjah kebebasan ini boleh difikirkan seperti berikut:

Andaikan kita ada penjumlahan n nilai:

Kita katakan x₁, x₂, …, x_n boleh mengambil sebarang nilai asalkan jumlahan adalah sifar. Bagaimanapun

sebenarnya kita boleh memperuntukkan sebarang nilai kepada n-1 dan yg terakhir akan mengambil nilai supaya jumlahan itu

sifar. Dlm keadaan ini, jumlahan itu dikatakan mempunyai darjah kebebasan n-1.