BAB4

(Konsep Kebarangkalian & Pengujian Hipotesis)

Konsep Kebarangkalian:

q Seringkali kita menyatakan sesuatu peristiwa itu dengan diikuti tahap keyakinan

q Contoh: Kita 70% yakin yang hujan akan turun dengan lebatnya hari ini; Kita hanya 5% yakin yg penyakit si Pulan akan sembuh.

q Kenyataan-kenyataan spt. di atas adalah kenyataan yg melibatkan pernyataan kebarangkalian

q Kebarangkalian sesuatu peristiwa ditakrifkan sebagai kebolehjadian peristiwa itu berlaku; Ini boleh dinyatakan dlm bentuk peratusan atau nombor antara 0 dan 1.

q Kita katakan peristiwa yang mempunyai kebarangkalian 100% atau 1 adalah peristiwa yg PASTI berlaku dan peristiwa yang mempunyai kebarangkalian 0 adalah MUSTAHIL untuk berlaku.

Pengiraan Kebarangkalian:

q Kebarangkalian, Kb boleh dikira berdasarkan:

Kb(Peristiwa A) = Bil. Peristiwa A yg mungkin ÷ Bil. Populasi.

q Contoh: Aktiviti melambung duit siling yang adil dan merekodkan keputusannya.

Keputusan yang mungkin atau populasi ={K,E}

Jika kita takrifkan Peristiwa A sebagai mendaptkan kepala iaitu

Peristiwa A={K}, maka Peristiwa A adalah subset kepada populasi

Dan

Kb({K})=n({K})/n({K,E})=1/2=0.5.

q Contoh:

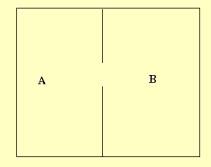
Sebuah kotak dibahagi 2, Petak A dan B dengan lubang yang menghubungkan antara keduanya. Petak A mengandungi 100 ekor lalat, dan 5 daripadanya yg dipilih secara rambang dan diwarnakan.

Kita berminat kepada peristiwa lalat berwarna adalah yg pertama memasuki Petak B.

Maka Kb(Lalat Pertama Memasuki Petak B adalah Lalat Berwarna)

=Bil. Lalat Berwarna ÷ Bil. Semua Lalat

=5/100

=0.05 atau 5 %.

Kita katakan terdapat 5% kemungkinan (atau kebarangkalian) yg lalat pertama memasuki petak B adalah lalat berwarna.

Peristiwa Mungkin Tak Berlaku (unlikely events):

q Bagi contoh kedua di atas, kerana hanya 5 ekor lalat yang diwarnakan, mungkin orang biasa berkata, peristiwa lalat yg pertama memasuki petak B adalah lalat berwarna mungkin tak berlaku.

q Kebarangkalian 5% atau kurang menunjukkan peristiwa mungkin tak berlaku; Bagimana pula dgn 10%, 15% dsb, adakah juga dikategorikan sebagai mungkin tak berlaku ?

q Orang biasa mungkin mempunyai presipsi berbeza tetapi ahli sains (penyelidik) bersetuju peristiwa yg mungkin tak berlaku itu mempunyai kebarangkalian 5% atau kurang.

q Bagaimanapun mungkin ada keadaan tertentu “Mungkin Tak Berlaku” ditakrifkan dgn nilai melebihi 5%, contoh 10%.

q Kebarangkalian “Mungkin Tak Berlaku” ini dipanggil paras keertian atau dengan tandaan a atau nilai-p.

Pengujian Hipotessis:

q Hipotesis adalah satu pernyataan atau penerangan yg dicadangkan berkaitan dgn sesuatu atau beberapa fakta.

q Contoh: Hipotesis bumi itu bulat menerangkan fakta yg kapal akan tidak kelihatan diufuk.

q Utk hipotesis diterima, ia mesti diuji kesahihannya dan ia mesti sahih dalam setiap pengujian.

q Hipotesis yg kuat masih sahih walaupun dilakukan pelbagai pengujian.

q Jika sesuatu hipotesis itu menjadi tidak sahih, ia perlu diperbaiki.

q Semak Contoh Dlm Biologi ini utk kefahaman lanjut:

Hipotesis Satu Hujung dan Dua Hujung:

q Pengujian dalam contoh di atas boleh ditulis dalam bentuk matematik.

H_o:m_A=m_B lwn. H_a :m_A¹m_B

Hipotesis seperti ini dipanggil dua hujung.

q Hipotesis boleh juga berbentuk:

H_o:m_A³m_B lwn. H_a :m_A<m_B

Atau

H_o:m_A£m_B lwn. H_a :m_A>m_B

Hipotesis sebegini dipanggil hipotesis satu hujung.

Kajian Secara eksperimen dan kajian secara pemerhatian:

q Dalam contoh di atas di mana hipotesis alternatif diterima, kita katakan data menyokong hipotesis ini:

q Bagaimanapun data juga menyokong hipotesis alternatif lain spt:

· Banyak makanan di hulu & dgn itu ikan lebih berat di kawasan berkenaan.

· Habitat di hilir lebih sesuai kpd pemangsa berbanding di hulu.

dsb.

q Dgn perkataan lain, data menyokong hipotesis-hipotesis tersebut tetapi tidak menyatakan yang pencemaran menyebabkan tumbesaran ikan terbantut secara spesifik. Ini membawa kepada konsep CAUSE and EFFECT.

q Dalam kajian ini kita tidak dapat menentukan hubungan CAUSE and EFFECT ini. Kajian ini dipanggil sebagai Kajian Secara Pemerhatian.

q Untuk menentukan hubungan CAUSE and EFFECT ini, perlu dijalankan Kajian Secara Eksperimen & bahagian ini akan diajar oleh Dr Yosni Bakar.

Prosedur Pengujian Hipotesis:

q Dalam contoh di atas, masih kurang jelas bagaimana prosedur pengujian hipotesis dijalankan, bagaimana kita menolak atau menerima sesuatu hipotesis, dsb.

q Dalam pengujian hipotesis bertentangan iaitu Hipotesis Nol H_o lwn. Hipotesis Alternatif H_a, DUA ralat mungkin berlaku iaitu Ralat Jenis I dan Ralat Jenis II.

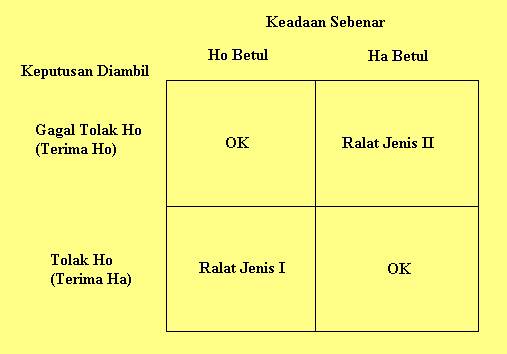
Ralat Jenis I = Ralat di mana H_o ditolak walhal H_o adalah betul

Ralat Jenis II= Ralat H_o gagal ditolak walhal H_o salah.

Dalam proses pengujian hipotesis, kita berkemungkinan melakukan Ralat Jenis I jika kita menerima Ha (menolak H_o) atau berkemungkinan melakukan Ralat Jenis II jika kita menerima H_o.

Tandaan:

a=Kb(Ralat Jenis I)

b=Kb(Ralat Jenis II)

Prosedur pengujian perlu dilakukan supaya a dan b, adalah sekecil mungkin.

Konsep ini diperjelaskan dengan contoh mudah pengujian hipotesis berikut:

Andaikan X ~ N(m,16). Andaikan kita berminat membuat pengujian hipotesis

berikut:

H_o: m=10 lwn. H_a: m=11

Andaikan satu sampel bersaiz 25 dipungut dari populasi ini dan keputusan dibuat mengenai hipotesis di atas.

Apakah KRITERIA yang optimum untuk membuat keputusan? OPTIMUM di sini bermakna kedua-dua a dan b sekecil mungkin.

Dalam menentukan kriteria ini, kita boleh memilih a secara langsung, iaitu kb kita melakukan Ralat Jenis I sekecil mungkin. (dgn perkataan lain dgn mengambil a sekecil mungkin, kita meletakkan peristiwa kita melakukan Ralat Jenis I kepada kategori “Mungkin Tak Berlaku”)

Biasanya nilai a yang dipilih adalah 5% atau a=0.05.

Bagaimanapun b tidak boleh dipilih secara langsung. Kita boleh memilih KRITERIA PENOLAKAN atau KAWASAN PENOLAKAN (atau KAWASAN GENTING) supaya b sekecil mungkin.

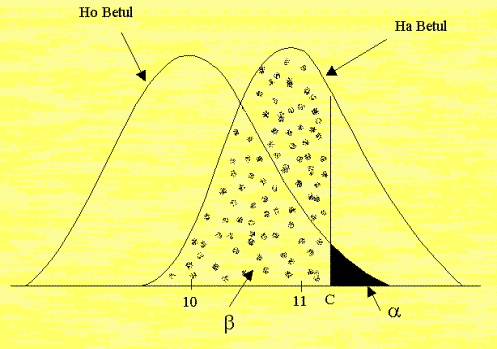
Set 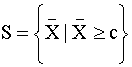dipanggil sebagai Kawasan Penolakan. Iaitu jika min sampel sama atau melebihi nilai c, maka Ho akan ditolak.

Nilai c boleh ditentukan untuk sesuatu nilai a.

Untuk memahami langkah ini, anda perlu memahami Teorem Kecenderungan Had Memusat (CLT)

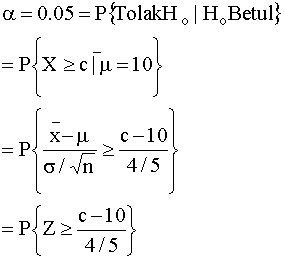
Daripada Jadual Taburan Normal Piawai,

P{Z³1.645}=0.05. Maka,

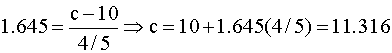
Maka Kawasan Penolakan Bagi pengujian ini adalah

Ho akan ditolak pada paras keertian a=0.05 jika min sampel yang dipungut memenuhi kriteria kawasan penolakan.

Apa kah b bagai kawasan penolakan ini?

Kawasan penolakan lain yang bersaiz sama (iaitu a=0.05) mungkin wujud tetapi nilai b mungkin lebih besar dan dengan itu tidak optimum.

Konsep pengujian hipotesis ini akan kita gunakan untuk perbincangan di bab yang seterusnya.

Uji Kefahaman Anda